La sezione aurea nella costruzione del marchio.
La sezione aurea
nella costruzione del marchio.
Ho il piacere e l’onore
di pubblicare in due puntate
il testo integrale
scritto nel 2008 da una ragazza
al termine del quinto anno
del liceo scientifico.
Il testo riguarda il percorso
pluridisciplinare di approfondimento
tra scienza, matematica, filosofia e arte.
La ragazza in questione, in seguito,
si è laureata in matematica
lavorando poi per 4 anni come ricercatrice
presso l’Università di Neuchatel
con tesi di dottorato su:
“Trace-zero subgroups of elliptic
and twisted Edwards curves:
a study for cryptographic applications.”
Lascio quindi spazio a Giulia Bianco
che, con gentilezza,
(vedi Sergione…)
ha avuto il merito di farmi comprendere
la bellezza dei numeri,
fondamento della natura
e base dei codici della Logogenesi.
Sergio Bianco
La matematica
non è una disciplina a se stante,
ma è presente in Natura,
nella realtà che ci circonda,
così come nell’Arte.
La sezione aurea è un numero
dato dalla relazione che intercorre
tra le due parti in cui è diviso un segmento.
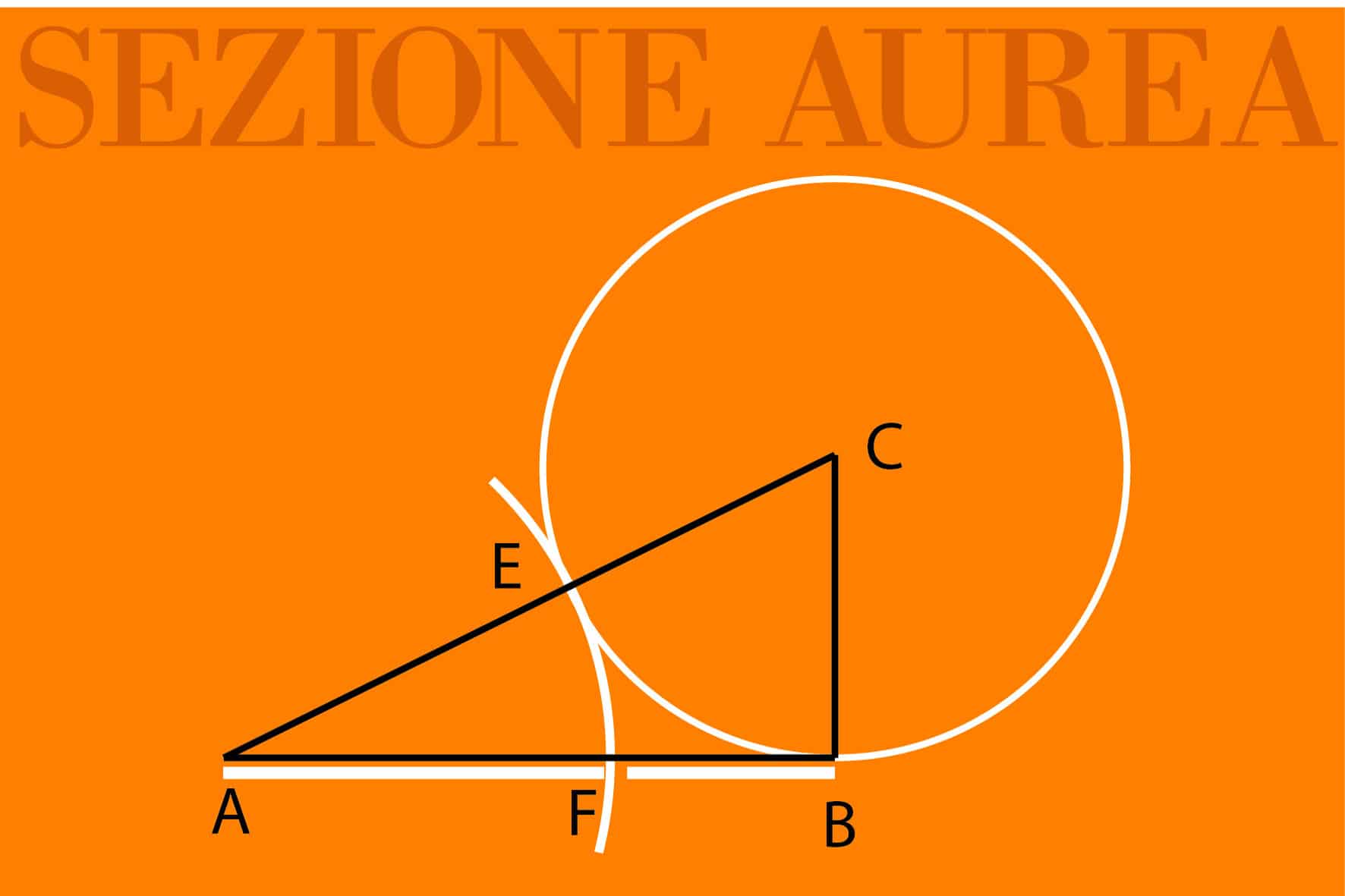
Geometricamente, la sezione aurea
si costruisce in questo modo:
Dato un segmento AB,
si traccia la perpendicolare in B di lunghezza CB,
pari a AB/2,
si traccia poi l’ipotenusa AC
del triangolo rettangolo così disegnato
e su di essa si segna il punto E,
ove passa la circonferenza di centro C e raggio CB.
Si riporta ora il segno con raggio AE su AB
definendo il segmento AF
medio proporzionale rispetto ad AB e FB.
Il rapporto tra AB e FB è pari a 1,618,
numero che rappresenta la sezione aurea.
Questo rapporto tra lunghezze
era già conosciuto nell’antichità
dai matematici greci.
Fu definito con chiarezza
per la prima volta da Euclide (terzo secolo a.C.),
che lo chiamò “proporzione estrema media”.
Il nome “sezione aurea”
comincia invece ad essere utilizzato
solo a partire dall’Ottocento.
Vi sono alcune figure geometriche
che si basano sulla sezione aurea:
ricordiamo il decagono
e il pentagono regolare.
Nel decagono regolare,
il lato è in sezione aurea
rispetto al raggio del cerchio circoscritto,
nel pentagono regolare,
il lato è in sezione aurea rispetto alla diagonale.
Un’altra figura che si basa sulla sezione aurea
è la spirale logaritmica,
che si costruisce con una serie di rettangoli aurei.
(il rettangolo aureo è un rettangolo
il cui lato è sezione aurea dell’altro).
Infine la sezione aurea
si ritrova nella successione di Fibonacci,
così chiamata dal nome del matematico
che la ideò, Leonardo Da Pisa detto Fibonacci.
La successione di Fibonacci
è una serie ricorsiva in cui ciascun termine,
a partire dal terzo,
è uguale alla somma
dei due termini precedenti:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Il rapporto fra un termine
e quello che lo precede
si avvicina sempre di più alla sezione aurea.
La sezione aurea
è presente frequentemente in Natura.
In botanica,
la sezione aurea si ritrova nel girasole
(il centro dell’infiorescenza del girasole
presenta spirali logaritmiche
orarie e antiorarie che si intersecano tra loro),
nella mela (tagliando la mela a metà
e congiungendo idealmente i suoi semi
si ottiene una stella a 5 punte),
nella pigna e nell’ananas
(le scaglie seguono l’andamento
della spirale logaritmica).
In zoologia, la sezione aurea
si ritrova nella stella marina
(una stella a cinque punte),
nel Nautilus, la cui conchiglia
ha la forma di una spirale logaritmica.
(infatti la spirale logaritmica
presenta la particolare proprietà
dell’autosomiglianza,
per cui, crescendo, non cambia forma,
così che il Nautilus può ampliare la sua dimora,
senza modificarne l’equilibrio).
Il falco pellegrino, durante la caccia,
segue l’andamento di una spirale logaritmica
per calare sulla preda
(infatti gli occhi del falco guardano di lato
e questo andamento gli permette
di non perdere di vista l’obiettivo).
Infine, la sezione aurea
si ritrova anche nel cosmo,
nelle galassie che seguono
l’andamento di una spirale logaritmica. (segue domani)
Giulia Bianco
Fine della prima parte
La seconda, riguardante la sezione aurea
e il mondo dell’arte, sarà pubblicata domani.
Grazie dell’Attenzione.
